
“微信扫一扫”进入题库练习及模拟考试
初中数学八年级上册试题库(555题)
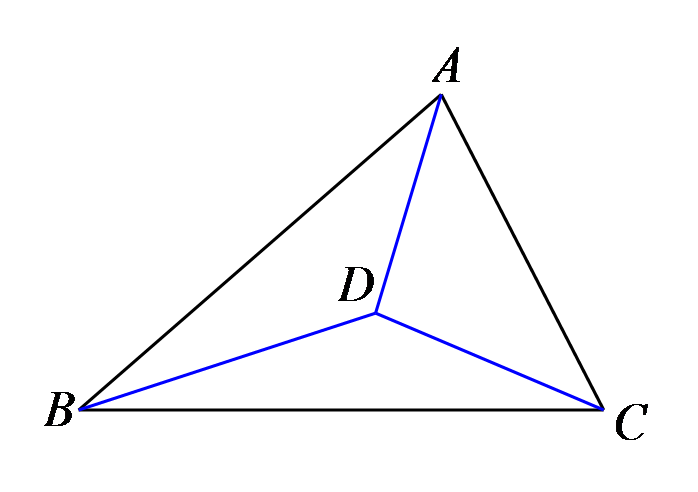
已知:如图,点D是
求证:
(1)BD+CD<AB+AC;
(2)AD+BD+CD<AB+BC+AC。
知识点:第十一章 三角形
参考答案:
证明:(1)延长
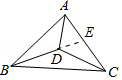
在
在
(2)由(1)同理可得:

“微信扫一扫”进入题库练习及模拟考试
已知:如图,点D是
求证:
(1)BD+CD<AB+AC;
(2)AD+BD+CD<AB+BC+AC。

参考答案:
证明:(1)延长

在
在
(2)由(1)同理可得: