
“微信扫一扫”进入题库练习及模拟考试
高中数学选择性必修 第二册(381题)
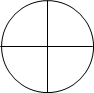
把圆分成
猜想
知识点:第四章 数列
参考答案:当 \(n \geqslant 4\) 时,首先,对于第1个扇形 \({a_1}\) ,有4种不同的染法,由于第2个扇形 \({a_2}\) 的颜色与 \({a_1}\) 的颜色不同,所以,对于 \({a_2}\) 有3种不同的染法,类似地,对扇形 \({a_3}\),…,\({a_{n - 1}}\) 均有3种染法.对于扇形 \({a_n}\) ,用与 \({a_{n - 1}}\) 不同的3种颜色染色,但是,这样也包括了它与扇形 \({a_1}\) 颜色相同的情况,而扇形 \({a_1}\) 与扇形 \({a_n}\) 颜色相同的不同染色方法数就是 \(f\left( {n - 1} \right)\) ,于是可得 \(f\left( n \right) = 4 \times {3^{n - 1}} - f\left( {n - 1} \right)\) 猜想 \(f\left( n \right) = {3^n} + {\left( { - 1} \right)^n} \cdot 3\) 当 \(n = 3\) 时,左边 \(f\left( 3 \right) = 24\) ,右边 \({3^3} + {\left( { - 1} \right)^3} \cdot 3 = 24\) ,所以等式成立假设 \(n = k\left( {k \geqslant 3} \right)\) 时, \(f\left( k \right) = {3^k} + {\left( { - 1} \right)^k} \cdot 3\) ,则 \(n = k + 1\) 时, \(f\left( {k + 1} \right) = 4 \times {3^k} - f\left( k \right) = 4 \times {3^k} - {3^k} - {\left( { - 1} \right)^k} \cdot 3\) \( = {3^{k + 1}} + {\left( { - 1} \right)^{k + 1}} \cdot 3\) 即 \(n = k + 1\) 时,等式也成立综上 \(f\left( n \right) = {3^n} + {\left( { - 1} \right)^n} \cdot 3\) \(\left( {n \geqslant 3} \right)\) 点睛:本题考查考查归纳分析能力,考查数学归纳法的应用,属中档题.