
“微信扫一扫”进入题库练习及模拟考试
高中数学选择性必修 第一册(264题)
为了开发古城旅游观光资源,镇政府决定在护城河上建一座圆形拱桥,河面跨度
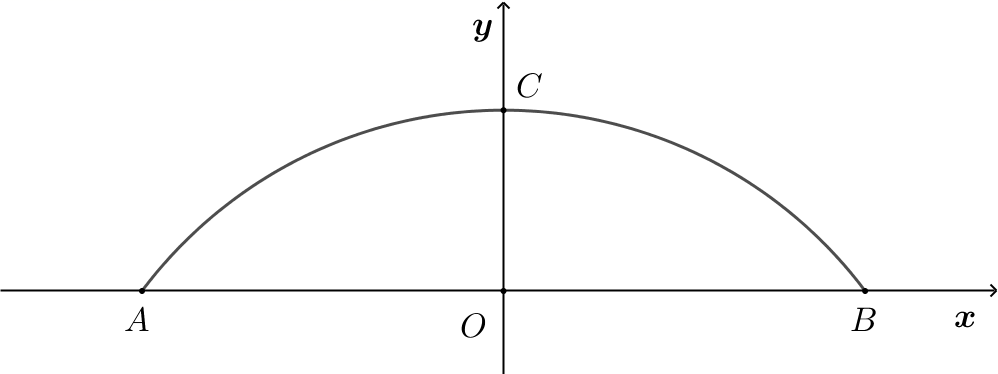
如果以跨度
知识点:第二章 直线和圆的方程
参考答案:\(B\left( {16,0} \right),C\left( {0,8} \right)\),
设圆心\(\left( {0,b} \right)\),
圆的方程为:\({x}^{2}+(y-b{)}^{2}={r}^{2}\),
由圆过点\(B\)、\(C\)可得\(\left \{ \begin{gathered} {(8-b{)}^{2}={r}^{2}} \\ {256+{b}^{2}={r}^{2}} \end{gathered} \right .\),
解得\(b=-12\),\(r=20\).
∴拱桥所在的圆方程是:\({x}^{2}+(y+12{)}^{2}=400\)
解析: