
“微信扫一扫”进入题库练习及模拟考试
高中数学 必修 第二册(415题)
为了监控某种零件的一条生产线的生产过程,检验员每隔30 min从该生产线上随机抽取一个零件,并测量其尺寸(单位:cm).下面是检验员在一天内依次抽取的16个零件的尺寸:

经计算得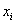 为抽取的第个零件的尺寸,
为抽取的第个零件的尺寸,
在
附:
知识点:第九章 统计
参考答案:均值为10.02方差为0.09

“微信扫一扫”进入题库练习及模拟考试
为了监控某种零件的一条生产线的生产过程,检验员每隔30 min从该生产线上随机抽取一个零件,并测量其尺寸(单位:cm).下面是检验员在一天内依次抽取的16个零件的尺寸:

经计算得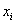 为抽取的第个零件的尺寸,
为抽取的第个零件的尺寸,
在
附:
参考答案:均值为10.02方差为0.09