
“微信扫一扫”进入题库练习及模拟考试
初中数学八年级下册(648题)
如图,已知正方形
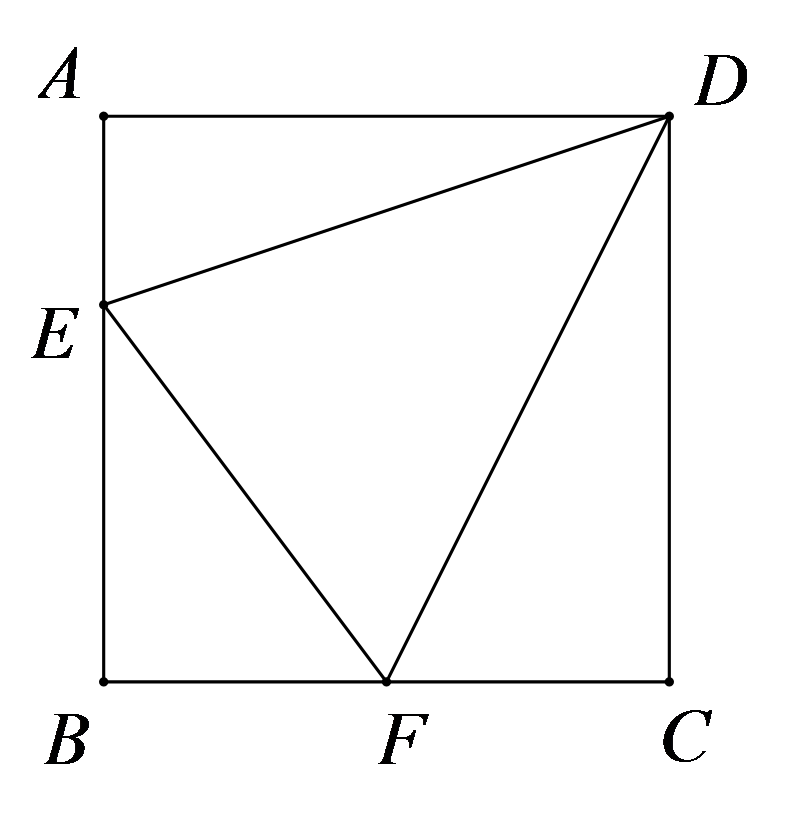
求证:\(EF = AE + CF\);
知识点:第十八章 平行四边形
参考答案:
延长
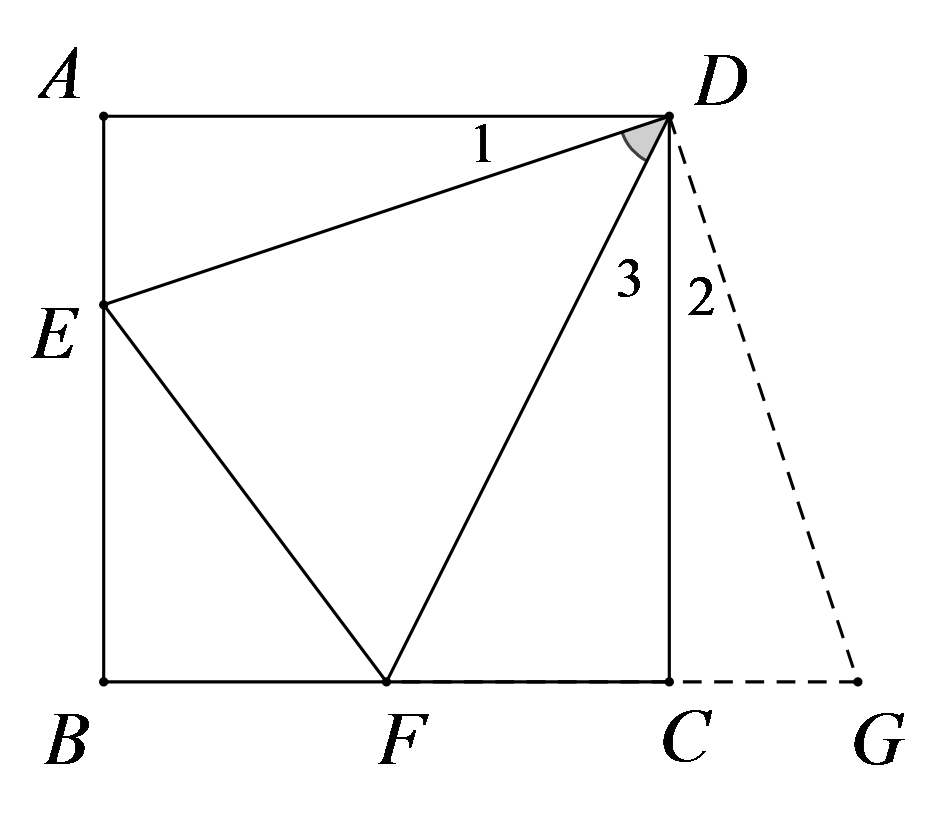
∵正方形
\(∠A=∠B=∠BCD=∠ADC=90°\)
∵在
∵在

“微信扫一扫”进入题库练习及模拟考试
如图,已知正方形
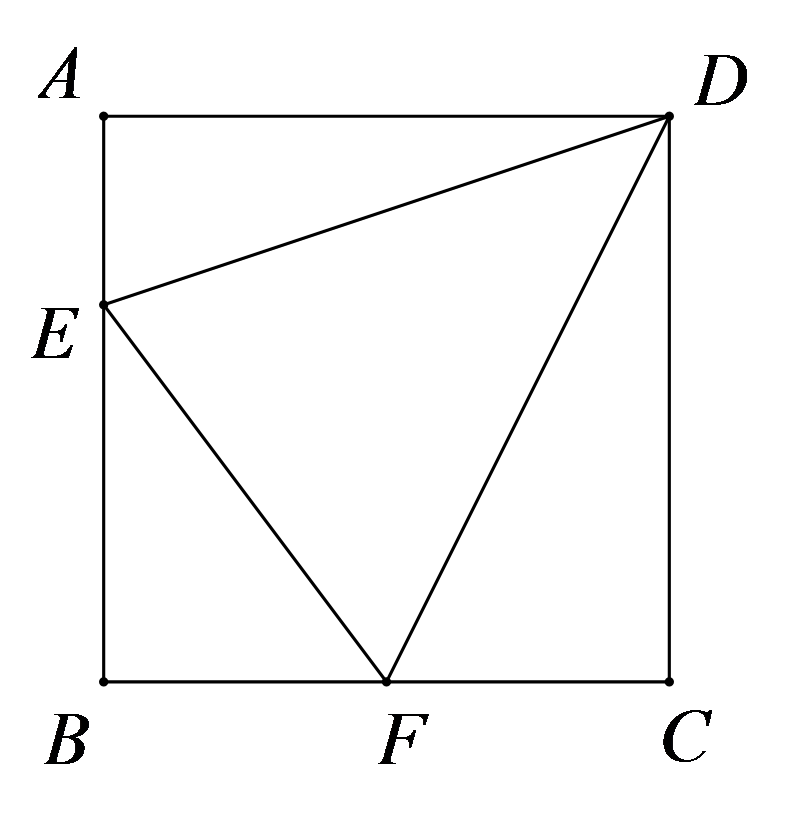
求证:\(EF = AE + CF\);
参考答案:
延长
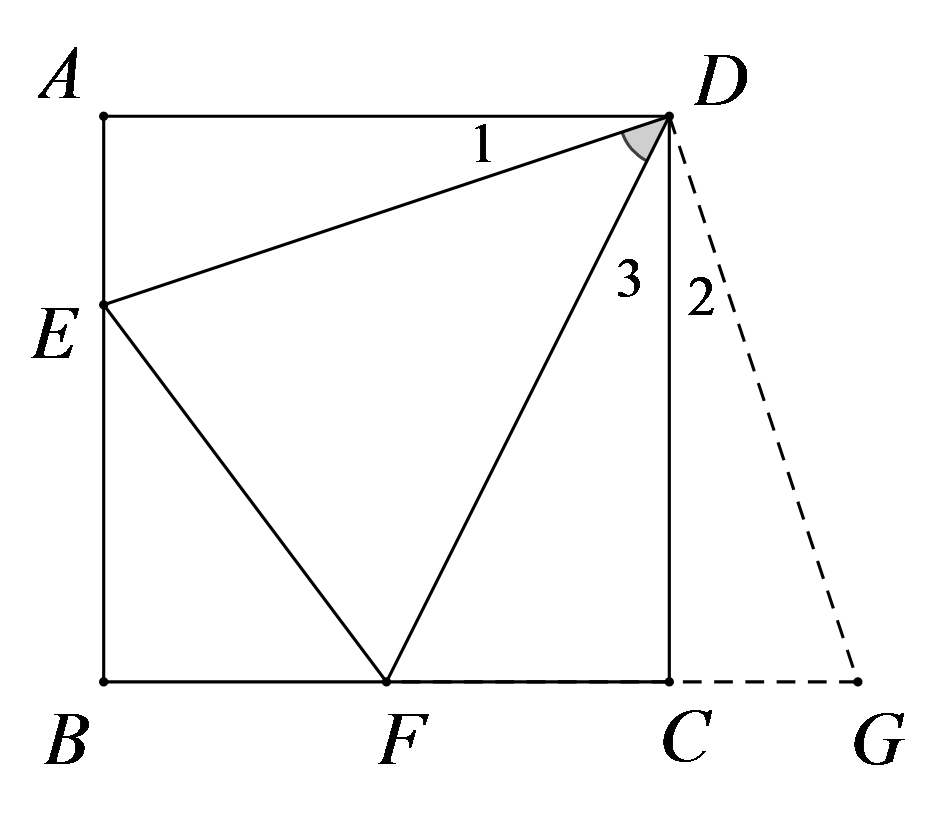
∵正方形
\(∠A=∠B=∠BCD=∠ADC=90°\)
∵在
∵在