
“微信扫一扫”进入题库练习及模拟考试
初中数学八年级下册(648题)
在正方形\(ABCD\)中,\(P\)为对角线\(BD\)上一点,\(PE \bot BC\),垂足为\(E\),\(PF \bot CD\),垂足为\(F\),求证:\(EF = AP\)。
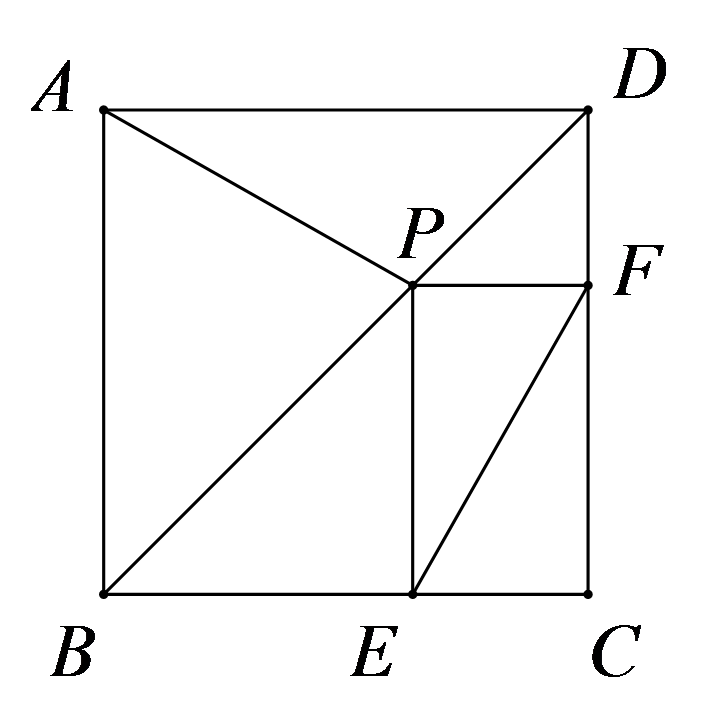
知识点:第十八章 平行四边形
参考答案:
证明:连接
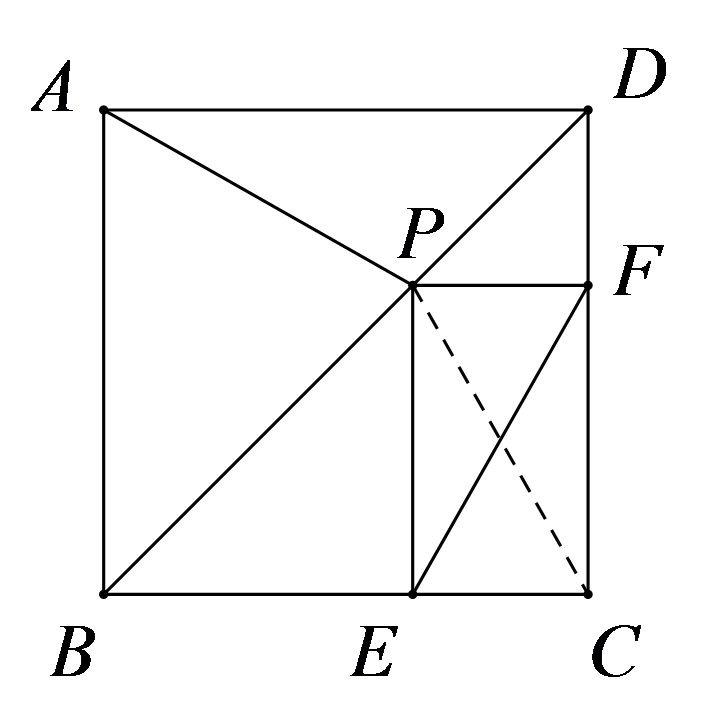
在
{AB = CB} \\
{\angle ABP = \angle CBP} \\
{BP = BP}
\end{array}} \right.\)

“微信扫一扫”进入题库练习及模拟考试
在正方形\(ABCD\)中,\(P\)为对角线\(BD\)上一点,\(PE \bot BC\),垂足为\(E\),\(PF \bot CD\),垂足为\(F\),求证:\(EF = AP\)。
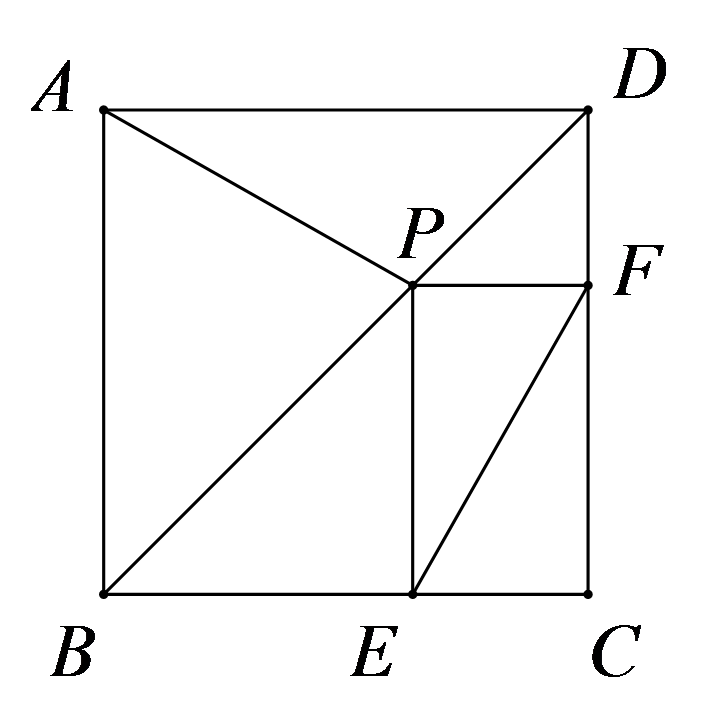
参考答案:
证明:连接
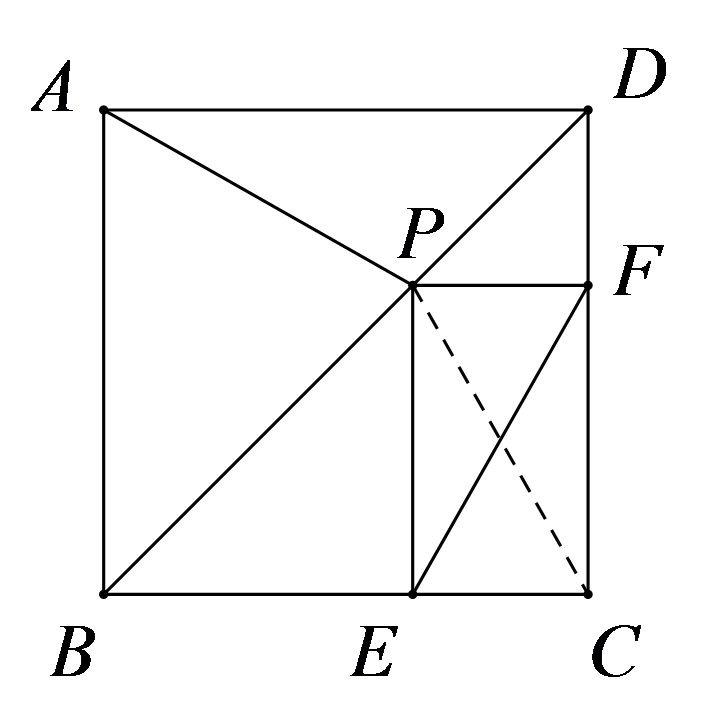
在
{AB = CB} \\
{\angle ABP = \angle CBP} \\
{BP = BP}
\end{array}} \right.\)