九年级（上）期末数学试卷集（328题）

---

二次函数y＝ax²＋bx＋c(a≠0)的部分图象如图所示，图象过点(－1，0)，对称轴为直线x＝2，下列结论：

(1)4a＋b＝0；

(2)9a＋c＞3b；

(3)8a＋7b＋2c＞0；

(4)若点A(－3，y₁)、点B、点C在该函数图象上，

则y₁＜y₃＜y₂；

(5)若方程a(x＋1)(x－5)＝－3的两根为x₁和x₂，且x₁＜x₂，则x₁＜－1＜5＜x₂.其中正确的结论有（    ）

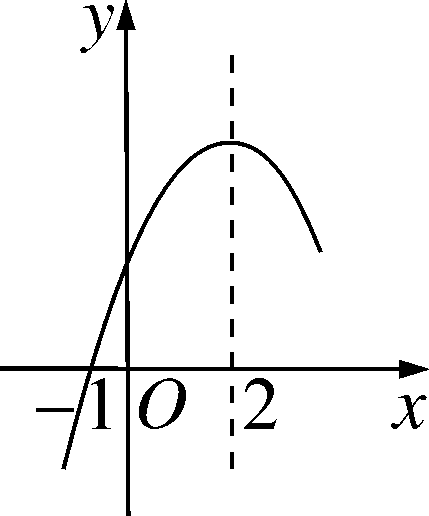
A.2个

B.3个

C.4个

D.5个

知识点：试卷13

参考答案：B

解析：

解析：∵－＝2，∴4a＋b＝0.故

（1）正确；∵x＝－3时，y＜0，∴9a－3b＋c＜0，∴9a＋c＜3b，故

（2）错误；由图象可知抛物线经过（－1，0）和（5，0），

∴

)∴8a＋7b＋2c＝8a－28a－10a＝－30a.

∵a＜0，∴8a＋7b＋2c＞0，故（3）正确；

∵点A（－3，y₁）、

∴点C离对称轴的距离近，

∴y₃＞y₂.∵a＜0，－3＜－＜2，∴y₁＜y₂，∴y₁＜y₂＜y₃，故（4）错误；∵a＜0，∴（x＋1）（x－5）＝－＞0，即（x＋1）（x－5）＞0，故x＜－1或x＞5，故（5）正确.∴正确的结论有三个，故选B.