“微信扫一扫”进入题库练习及模拟考试
九年级（上）期末数学试卷集（328题）
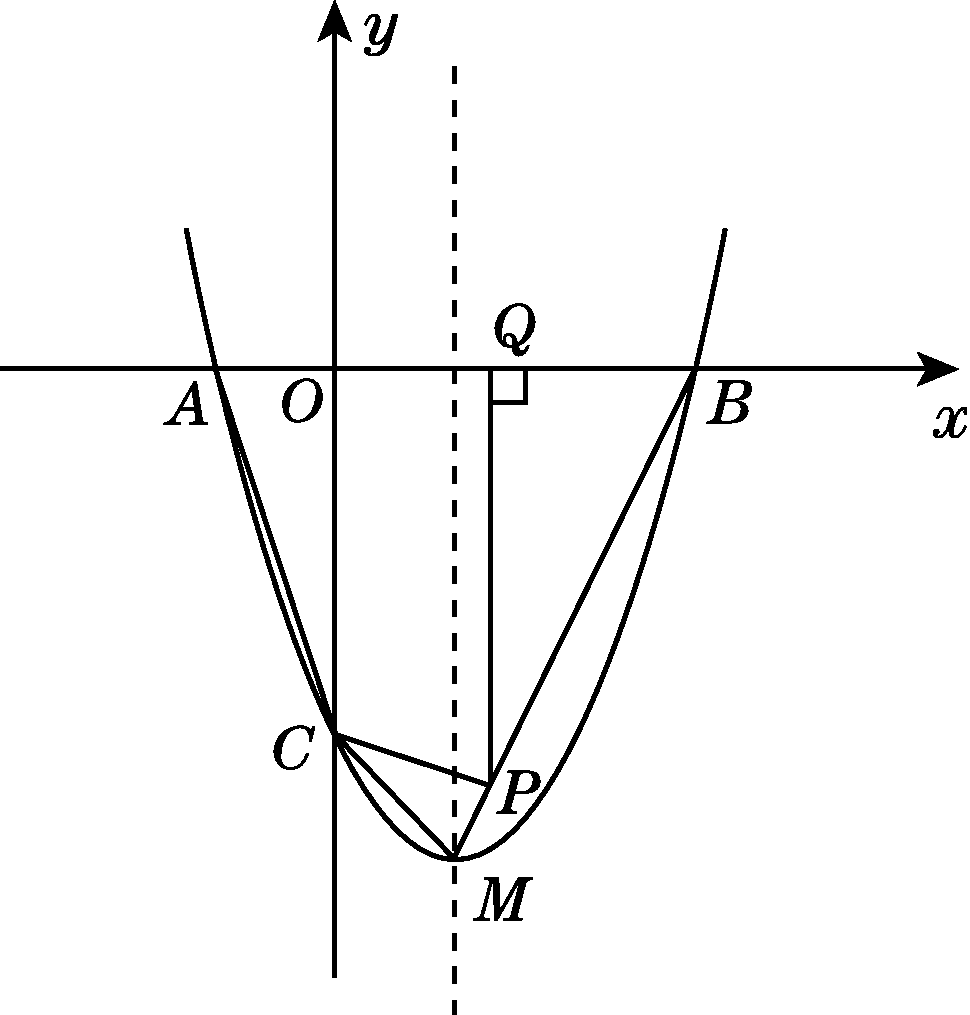
如图，抛物线y＝ax2＋bx＋c与x轴交于A，B两点(点A在点B左侧)，与y轴交于点C，且当x＝0和x＝2时，y的值相等，直线y＝3x－7与这条抛物线交于两点，其中一点横坐标为4，另一点是这条抛物线的顶点M.
(1)求顶点M的坐标．
(2)求这条抛物线对应的函数解析式．
(3)P为线段BM上一点(P不与点B，M重合)，作PQ⊥x轴于点Q，连接PC，设OQ＝t，四边形PQAC的面积为S，求S与t的函数解析式，并直接写出t的取值范围．
(4)在线段BM上是否存在点N，使△NMC为等腰三角形？若存在，求出点N的坐标，若不存在，说明理由．
知识点：试卷12
参考答案：见解析
解析：
解：(1)∵当x＝0和x＝2时，y的值相等，∴抛物线的对称轴为直线x＝1.∴顶点M的横坐标为1.
又∵顶点M在直线y＝3x－7上，
∴y＝－4，∴M(1，－4)．
(2)把x＝4代入y＝3x－7，
解得y＝5，设抛物线对应的函数解析式为y＝a(x－1)2－4，
将点(4，5)的坐标代入得a＝1，
∴抛物线对应的函数解析式为y＝(x－1)2－4，即y＝x2－2x－3.
(3)由y＝x2－2x－3，可得A(－1，0)，B(3，0)，C(0，－3)，
∴直线MB对应的函数解析式为y＝2x－6，∴P(t，2t－6)．
∴S＝
×1×3＋(3＋6－2t)t，即S＝－t2＋
t＋
(1＜t＜3)．
(4)存在．假设存在这样的点N，使△NMC为等腰三角形．
∵点N在BM上，∴不妨设N点的坐标为(m，2m－6)且1<m<3，
则CM2＝12＋12＝2，CN2＝m2＋(2m－6＋3)2，MN2＝(m－1)2＋(2m－6＋4)2.
△NMC为等腰三角形，有以下三种可能：
①若CN＝CM，则m2＋(2m－6＋3)2＝2，解得m＝
或m＝1(舍去)，
∴
②若CM＝MN，则(m－1)2＋(2m－6＋4)2＝2，解得m＝1±
.
∵1<m<3，∴m＝1－舍去．
∴
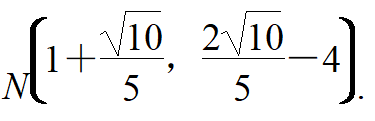
③若CN＝MN，则m2＋(2m－6＋3)2＝(m－1)2＋(2m－6＋4)2.解得m＝2.∴N(2，－2)．
综上，点N的坐标为
或(2，－2)．