九年级（上）期末数学试卷集（328题）

---

某公司生产的一种健身产品在市场上受到普遍欢迎，每年可在国内、国外市场上全部售完，该公司这种健身产品的年产量为6千件，若在国内市场上销售，平均每件产品的利润y₁(元)与国内的销售数量x(千件)的关系为

y₁＝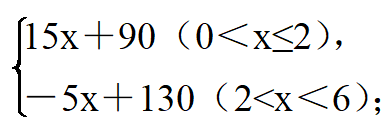

若在国外市场上销售，平均每件产品的利润y₂(元)与国外的销售数量t(千件)的关系为

y₂＝)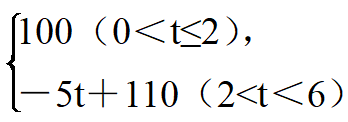

(1)用含x的代数式表示t为t＝__________；当0＜x<4时，y₂与x的函数解析式为y₂＝________________；当________≤x＜________时，y₂＝100.

(2)求每年该公司销售这种健身产品的总利润w(千元)与国内的销售数量x(千件)的函数解析式，并指出x的取值范围．

(3)该公司每年国内、国外的销售数量各为多少时，可使公司每年的总利润最大？最大值为多少？

知识点：试卷12

参考答案：见解析

解析：

解：(1)6－x；5x＋80；4；6

(2)当0<x≤2时，w＝(15x＋90)x＋(5x＋80)(6－x)＝10x²＋40x＋480；当2<x<4时，w＝(－5x＋130)x＋(5x＋80)(6－x)＝－10x²＋80x＋480；当4≤x<6时，w＝(－5x＋130)x＋100(6－x)＝－5x²＋30x＋600.综上所述，w＝)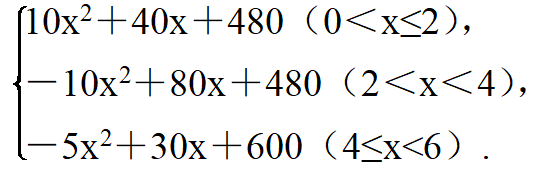

(3)当0<x≤2时，w＝10x²＋40x＋480＝10(x＋2)²＋440，

所以当x＝2时，w_最大值＝600；

当2<x＜4时，w＝－10x²＋80x＋480＝－10(x－4)²＋640，所以600＜w＜640；当4≤x<6时，w＝－5x²＋30x＋600＝－5(x－3)²＋645，所以当x＝4时，w_最大值＝640.

综上可知，当x＝4时，w_最大值＝640.

故当国内的销售数量为4千件，国外的销售数量为2千件时，可使公司每年的总利润最大，最大值为640千元．