九年级（上）期末数学试卷集（328题）

---

如图，AB为⊙O的直径，C为⊙O上一点，D是弧BC的中点，过点D作⊙O的切线交AC的延长线于点E，DE＝4，CE＝2.

(1)求证：DE⊥AE；

(2)求⊙O的半径．

知识点：试卷12

参考答案：见解析

解析：

(1)证明：如图，连接AD，OD.

∵DE是⊙O的切线，∴DE⊥OD.

∵OA＝OD，∴∠2＝∠3.∵D是弧BC的中点，∴BD(︵)＝CD(︵).∴∠1＝∠2.∴∠1＝∠3.∴OD∥AE.∴DE⊥AE.

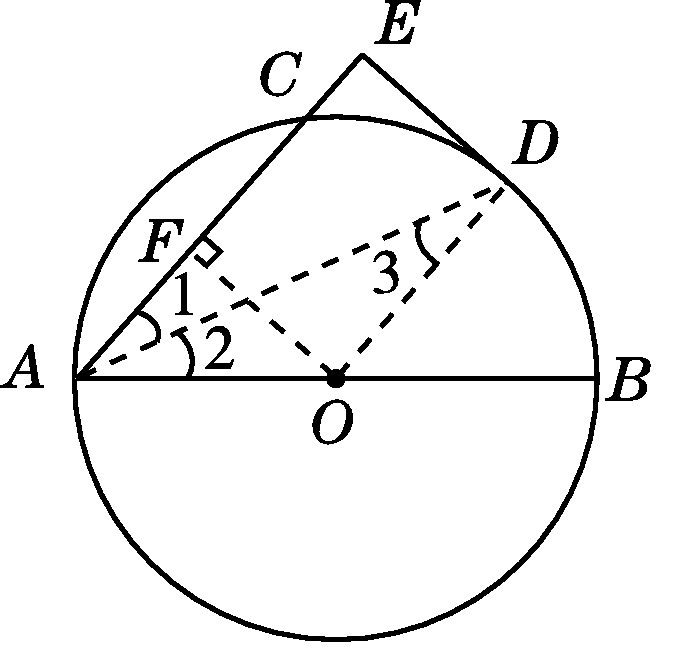
(2)解：如图，过点O作OF⊥AE于点F.易知四边形ODEF为矩形．

∴OF＝DE＝4，EF＝OD.

∵OF⊥AC，∴AF＝CF.

设⊙O的半径为x，

则AF＝CF＝EF－CE＝x－2.

在Rt△AFO中，AF²＋OF²＝AO²，

即(x－2)²＋4²＝x²，解得x＝5.

∴⊙O的半径为5.