八年级（上）期末数学试卷集（305题）

---

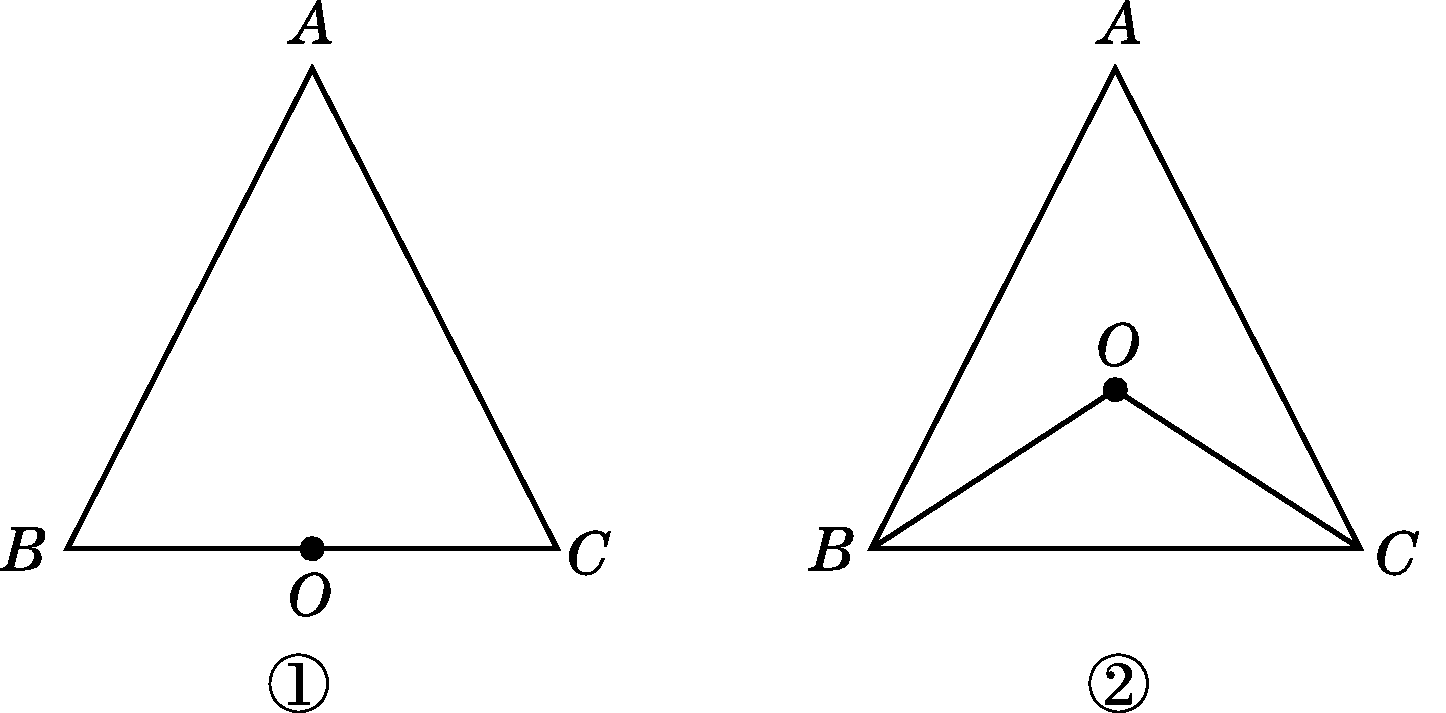
如图，已知点O到△ABC的两边AB，AC所在直线的距离相等，且OB＝OC.

(1)如图①，若点O在BC上，求证：△ABC是等腰三角形．

(2)如图②，若点O在△ABC内部，求证AB＝AC.

(3)若点O在△ABC的外部，AB＝AC还成立吗？请画图说明．

知识点：试卷12

参考答案：见解析

解析：

(1)证明：如图，过O作OE⊥AB于E，OF⊥AC于F，则∠OEB＝∠OFC＝90°.

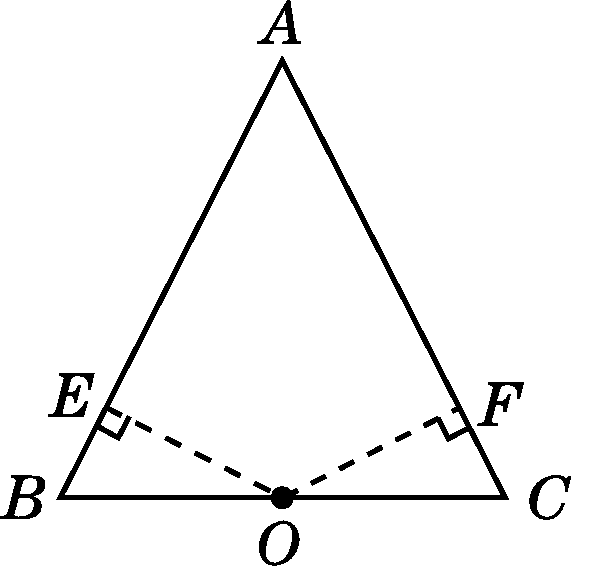(第26(1)题)

∵点O到△ABC的两边AB，AC所在直线的距离相等，

∴OE＝OF.

在Rt△OEB和Rt△OFC中，

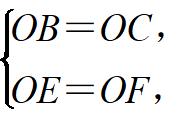
∴Rt△OEB≌Rt△OFC(HL)．

∴∠ABC＝∠ACB.

∴AB＝AC，

即△ABC是等腰三角形．

(2)证明：如图，过O作OE⊥AB于E，OF⊥AC于F，则∠OEB＝∠OFC＝90°.

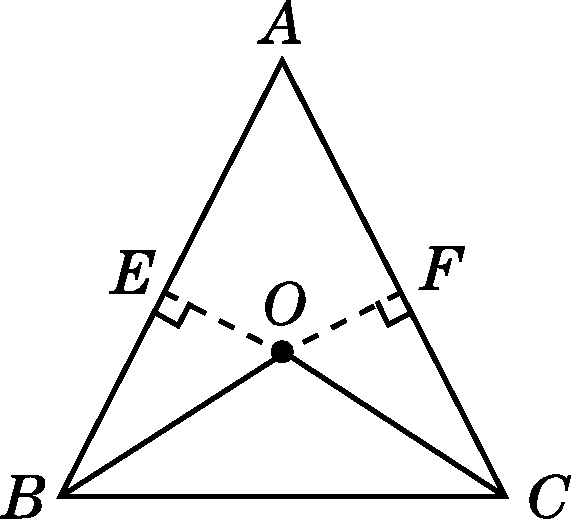(第26(2)题)

∵点O到△ABC的两边AB，AC所在直线的距离相等，

∴OE＝OF.

在Rt△OEB和Rt△OFC中，

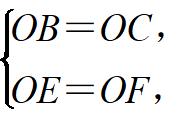
∴Rt△OEB≌Rt△OFC(HL)．

∴∠ABO＝∠ACO.

∵OB＝OC，∴∠OBC＝∠OCB.

∴∠ABC＝∠ACB.

∴AB＝AC.

(3)解：AB＝AC不一定成立．

理由：当∠BAC的平分线所在直线和BC的垂直平分线重合时，如图①，过O作OE⊥AB交AB的延长线于E，OF⊥AC交AC的延长线于F，则∠OEB＝∠OFC＝90°.

∵点O到△ABC的两边AB，AC所在直线的距离相等，

∴OE＝OF.

在Rt△OEB和Rt△OFC中，

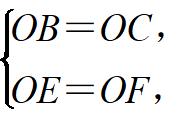
∴Rt△OEB≌Rt△OFC(HL)．

∴∠EBO＝∠FCO.

∵OB＝OC，

∴∠OBC＝∠OCB.

∵∠ABC＝180°－(∠OBC＋∠EBO)，

∠ACB＝180°－(∠OCB＋∠FCO)，

∴∠ABC＝∠ACB.

∴AB＝AC.

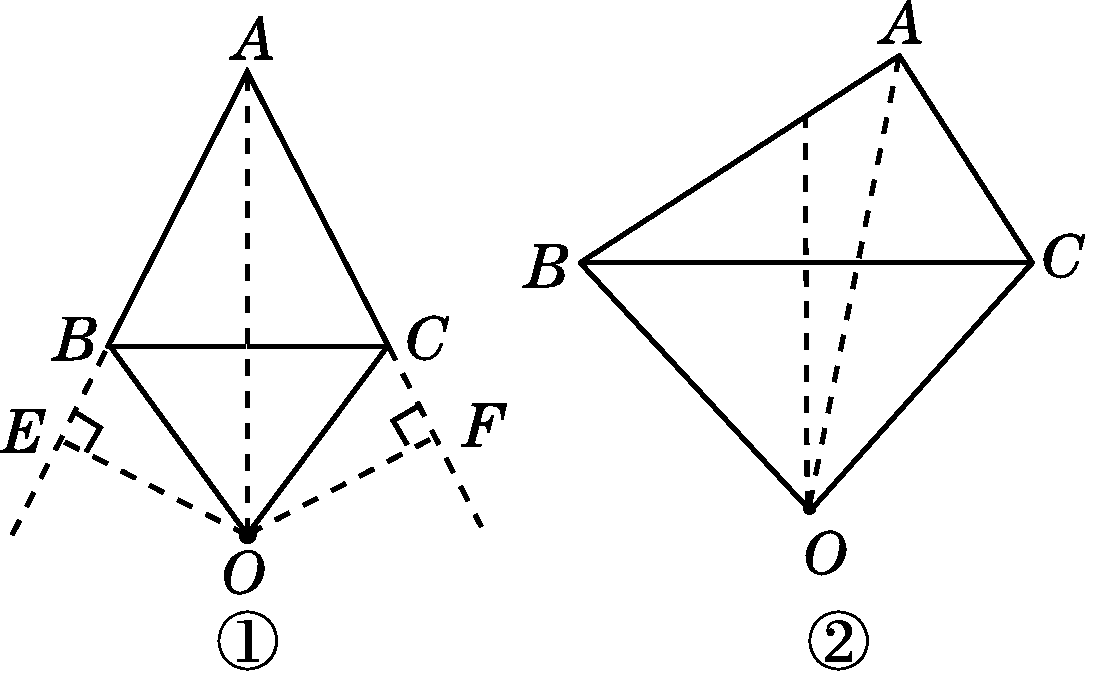(第26(3)题)

当∠BAC的平分线所在直线和BC的垂直平分线不重合时，如图②，∠ABC和∠ACB不相等，∴AB≠AC.

综上，AB＝AC不一定成立．