八年级（上）期末数学试卷集（305题）

---

如图，在△ABC中，AB＝BC ，DE⊥AB于点E，DF⊥BC于点D，交AC于点F.

(1)若∠AFD＝155°，求∠EDF的度数；

(2)若点F是AC的中点，求证∠CFD＝2(1)∠B.

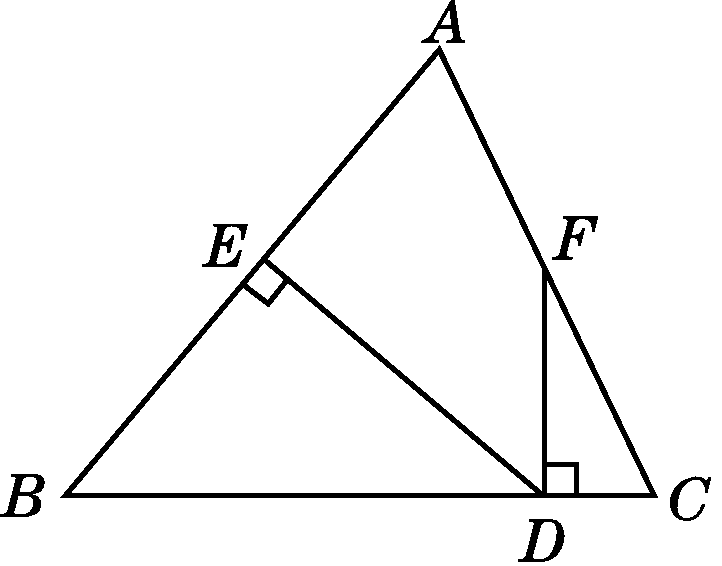
知识点：试卷12

参考答案：见解析

解析：

(1)解：∵∠AFD＝155°，

∴∠DFC＝25°.

∵DF⊥BC，DE⊥AB，

∴∠FDC＝∠AED＝90°.

∴∠C＝180°－90°－25°＝65°.

∵AB＝BC，

∴∠A＝∠C＝65°.

∴∠EDF＝360°－65°－155°－90°＝50°.

(2)证明：如图，连接BF.

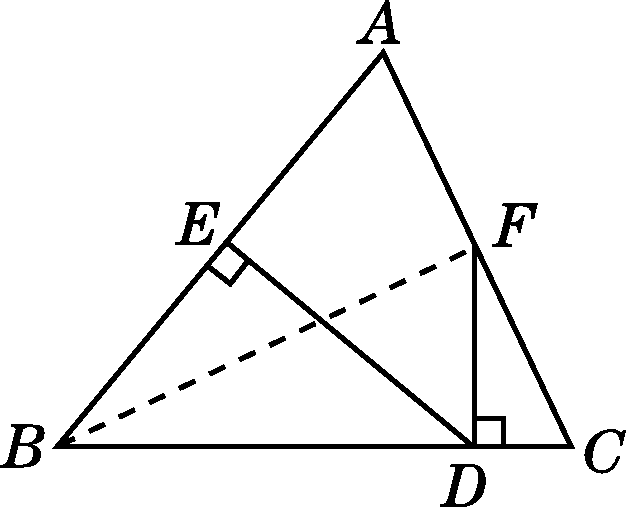(第24题)

 

 

∵AB＝BC，且点F是AC的中点，

∴BF⊥AC, ∠ABF＝∠CBF＝2(1)∠ABC.

∴∠CFD＋∠BFD＝90°.

∵FD⊥BC，

∴∠CBF＋∠BFD＝90°，

∴∠CFD＝∠CBF.

∴∠CFD＝2(1)∠ABC.