八年级（上）期末数学试卷集（305题）

---

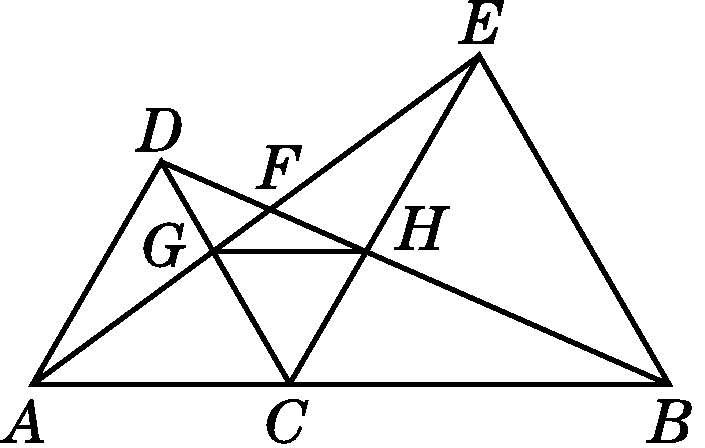
如图，C为线段AB上一动点(不与点A，B重合)，在AB同侧分别作正三角形ACD和正三角形BCE，AE与BD交于点F，AE与CD交于点G，BD与CE交于点H，连接GH.以下五个结论：①AE＝BD；②GH∥AB；③AD＝DH；④GE＝HB；⑤∠AFD＝60°，一定成立的是(　　)

A.①②③④

B.①②④⑤

C.①②③⑤

D.①③④⑤

知识点：试卷12

参考答案：B

解析：

点拨：∵△ACD和△BCE是等边三角形，∴AD＝AC＝CD，CE＝CB＝BE，∠ACD＝∠BCE＝60°.∵∠ACB＝180°，∴∠DCE＝60°.∴∠DCE＝∠BCE.

∵∠ACD＋∠DCE＝∠BCE＋∠DCE，∴∠ACE＝∠DCB.

在△ACE和△DCB中，

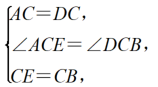
∴△ACE≌△DCB(SAS)．

∴AE＝BD，∠CAE＝∠CDB，∠AEC＝∠DBC.故①正确．

在△CEG和△CBH中，

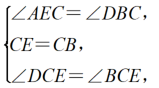
∴△CEG≌△CBH(ASA)，∴CG＝CH，GE＝HB，∴△CGH为等边三角形，∴∠GHC＝60°，

∴∠GHC＝∠BCH，∴GH∥AB.

故②④正确．

∵∠AFD＝∠EAB＋∠CBD，

∴∠AFD＝∠CDB＋∠CBD＝∠ACD＝60°.故⑤正确．

∵∠DHC＝∠HCB＋∠HBC＝60°＋∠HBC，∠DCH＝60°，

∴∠DCH≠∠DHC，∴CD≠DH，

∴AD≠DH.故③错误．

综上所述，正确的有①②④⑤.