八年级（上）期末数学试卷集（305题）

---

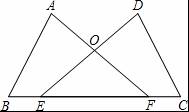
如图，点E，F在BC上，BE=CF，∠A=∠D，∠B=∠C，AF与DE交于点O．

（1）求证：AB=DC；

（2）试判断△OEF的形状，并说明理由．

知识点：试卷10

参考答案：见解析

解析：

【考点】全等三角形的判定与性质；等腰三角形的判定．

【专题】证明题．

【分析】（1）根据BE=CF得到BF=CE，又∠A=∠D，∠B=∠C，所以△ABF≌△DCE，根据全等三角形对应边相等即可得证；

（2）根据三角形全等得∠AFB=∠DEC，所以是等腰三角形．

【解答】（1）证明：∵BE=CF，

∴BE+EF=CF+EF，

即BF=CE．

又∵∠A=∠D，∠B=∠C，

∴△ABF≌△DCE（AAS），

∴AB=DC．

 

（2）解：△OEF为等腰三角形

理由如下：∵△ABF≌△DCE，

∴∠AFB=∠DEC，

∴OE=OF，

∴△OEF为等腰三角形．

【点评】本题主要考查三角形全等的判定和全等三角形对应角相等的性质及等腰三角形的判定；根据BE=CF得到BF=CE是证明三角形全等的关键．