八年级（上）期末数学试卷集（305题）

---

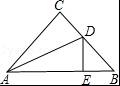
如图：△ABC中，∠C=90°，AC=BC，AD平分∠CAB交BC于D，DE⊥AB于E，且AB=6cm，则△DEB的周长是（　　）

A.6cm

B.4cm

C.10cm

D.以上都不对

知识点：试卷01

参考答案：A

解析：

【考点】角平分线的性质；等腰直角三角形．

【分析】由∠C=90°，根据垂直定义得到DC与AC垂直，又AD平分∠CAB交BC于D，DE⊥AB，利用角平分线定理得到DC=DE，再利用HL证明三角形ACD与三角形AED全等，根据全等三角形的对应边相等可得AC=AE，又AC=BC，可得BC=AE，然后由三角形BED的三边之和表示出三角形的周长，将其中的DE换为DC，由CD+DB=BC进行变形，再将BC换为AE，由AE+EB=AB，可得出三角形BDE的周长等于AB的长，由AB的长可得出周长．

【解答】解：∵∠C=90°，∴DC⊥AC，

又AD平分∠CAB交BC于D，DE⊥AB，

∴CD=ED，

在Rt△ACD和Rt△AED中，

，

∴Rt△ACD≌Rt△AED（HL），

∴AC=AE，又AC=BC，

∴AC=AE=BC，又AB=6cm，

∴△DEB的周长=DB+BE+ED=DB+CD+BE=BC+BE=AE+EB=AB=6cm．

故选A．