（三级）企业人力资源管理师专业技能试题（153题）

---

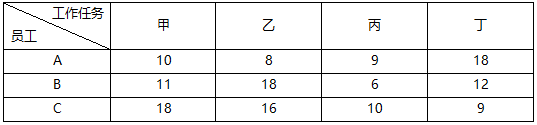
某车间产品装配组有甲、乙、丙、丁四名员工，现有A、B、C三项任务需要完成。在现有生产技术组织条件下，每位员工完成每项工作所需要的工时如表Ⅰ所示。

请运用匈牙利法求出员工与任务的配置方法，以保证完成任务的总时间最短，并求出完成任务的最短时间。

表Ⅰ       四名员工完成3项任务的工时统计表        单位：工时

知识点：第二章：招聘与配置

参考答案：见解析

解析：

P145，

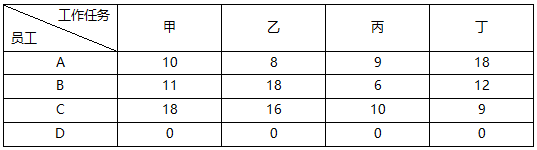
1.因员工数目多于任务数目，所以增添一项任务D，各员工完成任务E的时间均为0，详见表Ⅱ。

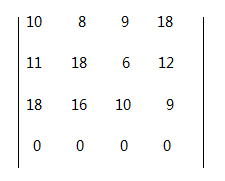
2.根据表Ⅱ，以各个员工完成各项任务的时间构造矩阵一。

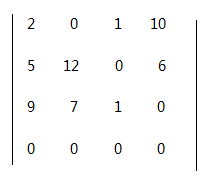
3.对矩阵一进行行约减，即每一行数据减去本行数据中的最小数，得到矩阵二。

4.矩阵二各行各列均有“0”，画“盖0”线。即画最少的线将矩阵二中的“0”全部覆盖住，得到矩阵三。

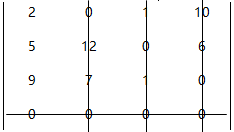
5.矩阵三的“盖0”线数目等于矩阵的维数。求最优解。

（1）先找只含一个“0”的行打“√”

（2）将带“√”的“0”所在列中的“0”打“×”

（3）重复第（1）（2）步至结束。

其结果如矩阵四所示，即乙员工负责A任务，丙员工负责B任务，丁员工负责C任务。

参照表Ⅰ四个员工完成任务的工时统计表，得出表Ⅲ，

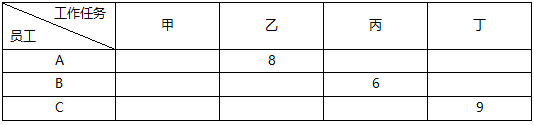
完成任务的最短时间是：8+6+9=23。