
“微信扫一扫”进入题库练习及模拟考试
一级造价工程师《建设工程案例分析》考试题库(33题)
某市为改善越江的交通状况,提出以下两个方案:
方案1:在原桥的基础上加固、扩建。该方案预计投资40 000万元,建成后可通行20年。这期间每年需维护费1 000万元。每10年需进行一次大修,每次大修费用为3 000万元。运营20年后报废时没有残值。
方案2:拆除原桥,在原址建一座新桥。该方案预计投资120 000万元,建成后可通行60年。这期间每年需维护费1 500万元。每20年需进行一次大修,每次大修费用为5 000万元,运营60年后报废时可回收残值5 000万元。
不考虑两方案建设期的差异,基准收益率为6%。
主管部门聘请专家对该桥应具备的功能进行了深入分析,认为应从F1、F2、F3、F4、F5共5个方面对功能进行评价。表2.1是专家采用0~4评分法对5个功能进行评分的部分结果,表2.2是专家对两个方案的5个功能的评分结果。
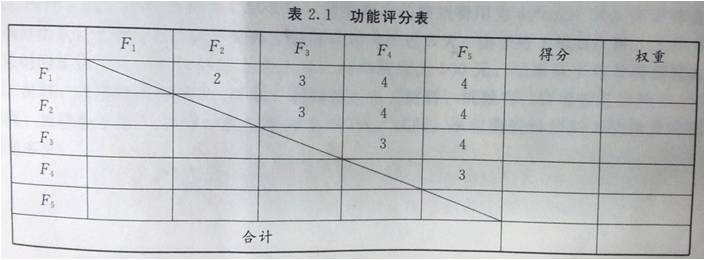

1.在表2.1中计算各功能的权重(权重计算结果保留三位小数)。
2.列式计算两方案的年费用(计算结果保留两位小数)。
3.若采用价值工程方法对两方案进行评价,分别列式计算两方案的成本指数(以年费用为基础)、功能指数和价值指数,并根据计算结果确定最终应入选的方案(计算结果保留三位小数)。
4.该桥梁未来将通过收取车辆通行费的方式收回投资和维持运营,若预计该桥梁的机动车年通行量不少于1 500万辆。分别列式计算两个方案每辆机动车的平均最低收费额(计算结果保留两位小数)。
知识点:第二章 工程设计、施工方案技术经济分析
参考答案:见解析
解析:
问题1:
功能分析表见表2.1。
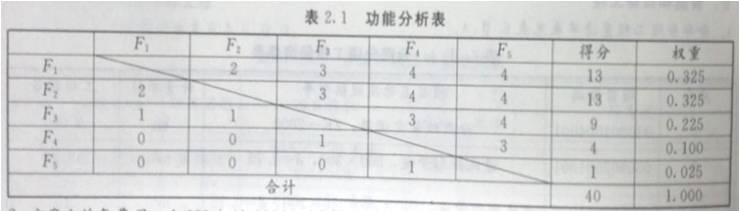
问题2:
方案1的年费用=1 000+40 000×(A/P,6%,20)+3 000×(P/F,6%,10)×(A/P,6%,20) =1 000+40 000×0.087 2+3 000×0.558 4×0.087 2=4 634.08(万元) 。
方案2的年费用=1 500+120 000×(A/P,6%,60)+5 000×(P/F,6%,20)×(A/P,6%,60)+5 000×(P/F,6%,40)×(A/P,6%,60)-5 000×(P/F,6%,60)×(A/P,6%,60) =1 500+120000×0.061 9+5 000×0.311 8×0.061 9+5 000×0.097 2×0.061 9-5 000×0.030 3×0.061 9=9 045.21(万元)。
问题3:
方案1的成本指数=4 634.08÷(4 634.08+9 045.21)=0.339。
方案2的成本指数=9 045.21÷(4 634.08+9 045.21)=0.661。
方案1的功能得分=6×0.325+7×0.325+6×0.225+9×0.100+9×0.025=6.700。
方案2的功能得分=10×0.325+9×0.325+7×0.225+8×0.100+9×0.025=8.775。
方案1的功能指数=6.700÷(6.700+8.775)=0.433。
方案2的功能指数=8.775÷(6.700+8.775)=0.567。
方案1的价值指数=0.433÷0.339=1.277。
方案2的价值指数=0.567÷0.661=0.858。
因为方案1的价值指数大于方案2的价值指数,所以应选择方案1。
问题4:
方案1的最低收费=4 634.08÷1 500=3.09(元/辆)。
方案2的最低收费=9 045.21÷1 500=6.03(元/辆)。